Tennis’s quirky scoring system can lead to some oddball results
Perhaps the most striking feature of tennis is its unique scoring system. It turns out that it’s not just a quirky flavour—the division of a match into points, games and sets actually affects the final results in some unexpected ways. For starters, tennis is one of the few games (the others being games with a similar structure like volleyball, table tennis and squash) in which the winner must win the final point of the match.
One of the other key features of the tennis scoring system is that, unlike sports such as cricket or football, not every point ultimately affects the outcome of the match. To see how this works, consider a match between Alice and Bob in which Alice is serving the first game of the first set. Alice wins the first three points, so at that stage the score is 40-0.
If Alice wins the next point, she wins the game, and the overall score for the match sits at 1-0.
But suppose Bob manages to score the next two points instead. The score sits at 40-30. Alice then wins the next point, she wins the game—and the overall score for the match again sits at 1-0. The same outcome occurs both times, regardless of whether or not Bob won his two points! Bob’s two points were effectively erased once Alice won the game, and have no influence whatsoever on the final outcome of the match.

This can lead to strange situations in which players can win more points than their opponents—or even more games—and yet still lose the match! This surprising result is closely related to a phenomenon in statistics called Simpson’s paradox, where looking at data in greater detail can lead to different conclusions compared with looking at data on a broad scale. How often does this actually occur in professional tennis matches? A study in 2013 set out to answer this question by analysing 61,000 professional tennis matches over a 21-year timespan. It found that about 4.5 per cent of games were won by the players with fewer overall points (so roughly 1 game in 22).
One of the most famous examples of this phenomenon occurred in the first round of Wimbledon in 2010, when American player John Isner defeated French player Nicolas Mahut, despite Isner winning fewer points overall (Isner won 478 points and Mahut won 502). The final score for the match was 6-4, 3-6, 6-7, 7-6, 70-68 (remember: no tie-breakers permitted in the fifth set at Wimbledon). This match also holds the record for the longest tennis match in history: 11 hours and 5 minutes spread across three days. A plaque commemorating this feat remains on Wimbledon Court 18.

Matches where the losing player wins more games (as opposed to points) are rarer, but still possible. In the final match of the 2009 Wimbledon Championship, Swiss player Roger Federer defeated American player Andy Roddick, despite Roddick winning 39 games to Federer’s 38 games. The final score was 5-7, 7-6, 7-6, 3-6, 16-14.
So why not switch to a simpler scoring system where only the total number of points matters? Tradition (and quirky flavour) aside, it turns out that the same mechanism that allows players to win with fewer points may also give consistently better players a better chance to win the match.
Winning probabilities
Mathematicians use Markov chains to analyse any system that moves from one state to another with certain probabilities. In his 1989 book Game, set and math, British mathematician Ian Stewart uses the mathematics of Markov chains to analyse a model tennis match. He found that if one player has probability p of winning any given point (which means their opponent has probability 1−p of winning any given point), then the probability that the player will win any given game is not p. Instead, it is given by the formula:
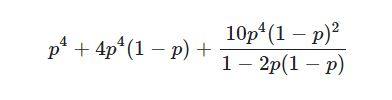
What does this mean? If p = 0.5, then both players are equally likely to win a point, and the probability that either player wins the game is also 0.5, as expected. However, the graph of this function has an interesting shape.
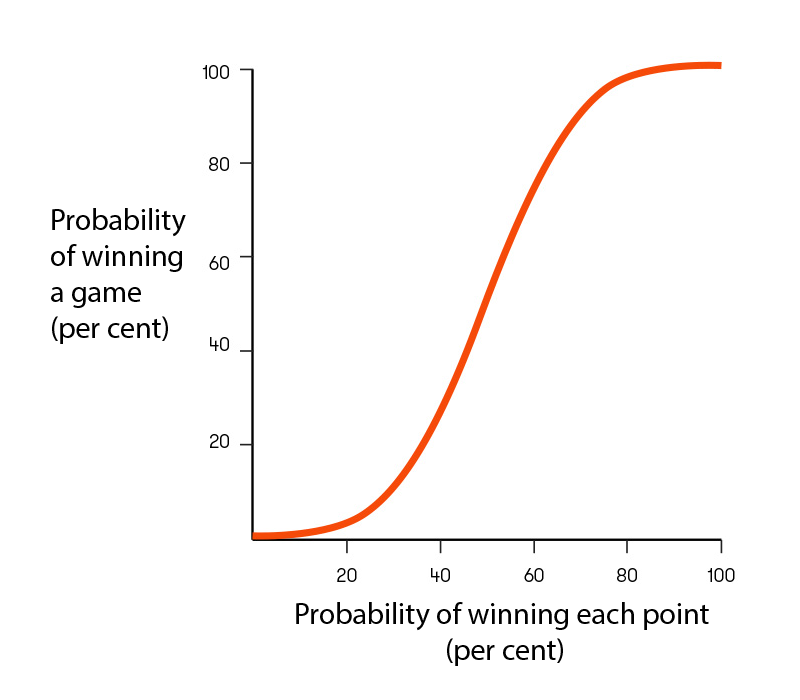
Stewart also found other formulas linking the probability of winning each individual point to the probabilities of winning sets and the match. The effect is magnified as we move from games to sets to matches.
This is only a simple model. In particular, an analysis of professional tennis matches shows that the probabilities of each player winning a given point does not stay the same throughout the match, but changes based on the outcomes of previous points. Nonetheless, it is useful to note that the scoring system of tennis rewards players who can maintain a consistent edge over their opponents, even if the edge is only small.