Two-Up: what are your chances?

If you walk into an Australian pub on Anzac Day, 25 April, there’s a pretty good chance you’ll find a crowd of people playing a fairly simple coin-tossing game: two-up. It’s a gambling game (and illegal for most of the year) with important cultural significance for Australians, as it was a popular pastime for Australian soldiers in the trenches and troop ships during World War I.

If two-up is new to you, here are the basics of how it works: a ‘spinner’ takes two coins (pennies were traditionally used) and places them on a small, flat piece of wood, called a kip. The rest of the players stand around the ‘ring’, a circle roughly 10 or 12 metres in diameter, and place bets on the outcome of the toss: heads (where both coins land with the ‘head’ side facing up), or tails (both coins land tails side up). The spinner steps inside the ring and tosses the coins at least three metres into the air, and they should land inside the ring. Play continues until either ‘heads’ or ‘tails’ are thrown—if ‘odds’ (one head and one tail) are thrown, there is no winner.

A crowd stands around waiting for someone to toss two coins on a wooden kip — Modern day games of two-up still often make use of pre-decimal era Australian pennies. Image adapted from: Newtown Graffiti / Flickr; CC-BY-2.0

It’s a game of pure chance, rather than skill. So, what’s the mathematics behind each toss of the coins?

To start with, let’s establish the probabilities of each separate coin toss. Although you’ve got ‘heads’, ‘tails’ and ‘odds’ to choose from, there are actually four possible ways for two coins to land:

Head, Head
Tail, Tail
Head, Tail
Tail, Head

Each of these outcomes has the same probability: 1 in 4, or 0.25, assuming that the coins are fair and not biased. This means the chances of getting ‘heads’ or ‘tails’ is always the same, at 1 in 4, or 25%. However, the chances of getting ‘odds’ is higher, thanks to there being two different paths to this outcome: 0.25 + 0.25 = 0.5, or 50%.

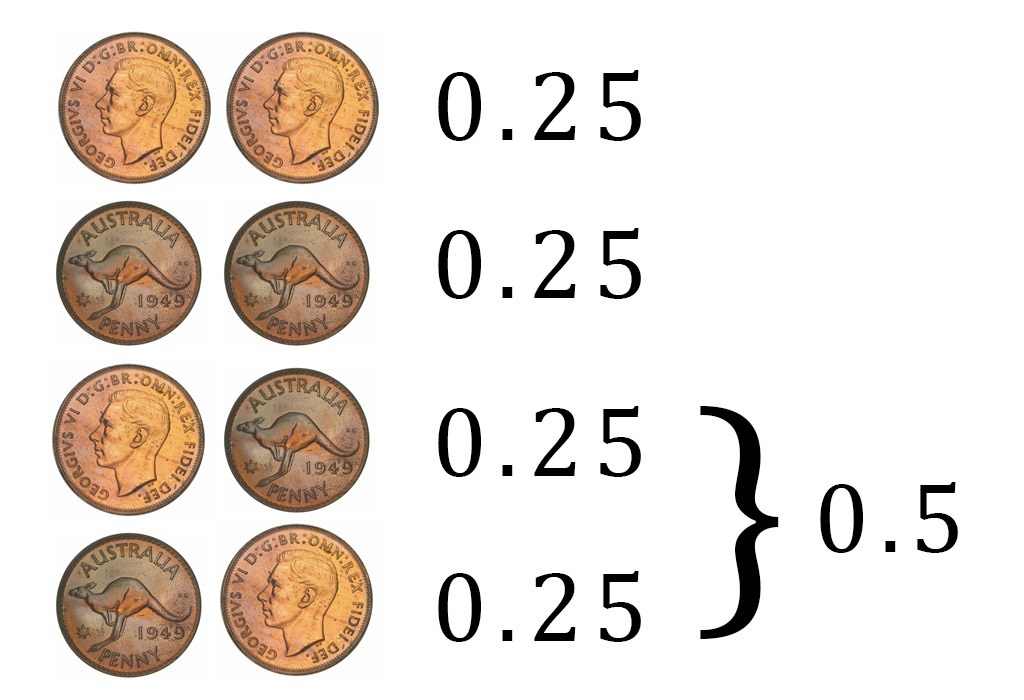
Illustration showing the probabilities of each coin toss result. — Image adapted from: Naomi Andrzejeski / Museum Victoria Collections; CC-BY-SA 4.0

Now, let’s say you’re watching the gameplay, and you notice something strange: the spinner has thrown ‘heads’ five times in a row. To calculate the chances of this happening, we can multiply the probability of throwing ‘heads’, by itself, five times:

P(heads) = 0.25

0.25 x 0.25 x 0.25 x 0.25 x 0.25 = 0.001 (rounded up - or 0.1%).

However, the probability of getting heads four times in a row and then tails is exactly the same:

P(heads) = 0.25

P(tails) = 0.25

0.25 x 0.25 x 0.25 x 0.25 x 0.25 = 0.001

As is the probability of getting heads, tails, heads, tails, heads:

0.25 x 0.25 x 0.25 x 0.25 x 0.25 = 0.001

Each coin toss is an independent event: the result of one coin toss does not influence the probabilities of any subsequent coin tosses. And yet, when we see something that seems strange and unlikely to us—like a run of five heads in a row—we think that, surely, the next throw must be tails! Why?

This effect is known as the ‘gambler’s fallacy’, where we believe that continuous runs of a particular outcome will later be balanced out by a tendency for the opposite outcome to occur, even for entirely random and independent events. In cognitive psychology terms, this is called ‘negative recency’. We tend to expect that random events will look random, regardless of whether we’re looking at a short series of events (like a run of five coin tosses) or a larger set of results (all the coin tosses for that day’s game). If something doesn’t look as random as we expect it should look, we get suspicious.

Interestingly, we tend to see the opposite effect, called the ‘hot hand’ effect or ‘positive recency’, where people are involved. For example, when a basketballer scores several times in a row, we think that they are more likely to keep scoring for all subsequent attempts. However, you could argue that the continued success of a skilled sportsperson makes more sense than a run of ‘heads’ results from inanimate objects.

A basketballer about to aim for the hoop — We perceive a big difference between a basketballer’s ‘hot streak’ and a sequence of identical coin tosses. Image adapted from: Tamarcus Brown; CC0

Why do we hold these fallacious beliefs about the randomness of a series of coin tosses? Some cognitive psychologists have suggested that this is partly influenced by the patterns we can see in other inanimate things in life. For example, if you're waiting for a freight train to go past while you're at a level crossing, it seems more and more likely with each passing carriage that the next carriage must surely be the final one. Eventually, of course, you're proven right: the final carriage passes.

Based on our prior experiences, we see these events happening in everyday life, and (perhaps incorrectly) assume that they will keep happening in other, different situations. It’s also very rare to encounter truly random events outside of casinos or playing games of chance, making us even more likely to fall for the gambler’s fallacy thinking.

While we may be good at identifying results from random events that seem highly unlikely, it seems we can still trick ourselves into making predictions based on faulty logic. It may be something to keep in mind if you find yourself at the pub on Anzac Day.

Always gamble responsibly. Gambling Help Online provides free support, information and counselling for Australian residents, or call 1800 858 858.