Planning the play-offs

Long before players set foot on the court, every match in their tournament needs to be scheduled. To decide how best to match up the players in the first round, the entrants to the tournament must first be seeded GLOSSARY seededA system to determine the order in which entrants are favoured to win a tournament, so they can be ‘planted’ into the appropriate tournament bracket. The 1st seed is the player deemed most likely to win, the 2nd seed is next-most likely to win, and so on, usually stopping at the 16th or 32nd seed. . The easiest way to seed the players is to look at their world rankings—but how are these determined in the first place?

World rankings

Every week the men's Association of Tennis Professionals (ATP) and the Women’s Tennis Association (WTA) compute and update the world rankings for professional tennis players. They do this by awarding ranking points to every player (separately for singles GLOSSARY singlesA tennis match played between two opposing players, using the inner set of sidelines to mark the left-right boundary of the court. —and doubles GLOSSARY doublesA tennis match played between two opposing pairs of players, using the outer set of sidelines to mark the left-right boundary of the court. —matches) then ranking players in order from most to fewest points. In order to rank doubles teams, the ranking points from both players in the team are simply added together.

How are the ranking points calculated? Each player’s best tournament results over the last 52 weeks are selected (though some important tournaments, such as the four Grand Slam tournaments, must be included in the calculation), and points are awarded for each tournament based on the type of tournament and how far the player progressed before being eliminated.

• Points awarded for men’s and women’s tournaments in 2016

  Listed below are the points awarded for tournaments in 2016.

  Tournament	Win GLOSSARY WinPlayer won the finals match and so won the tournament.	Finals GLOSSARY FinalsPlayer made it through to the 7th and final round (involving 2 players), but was eliminated there.	Semi-finals GLOSSARY Semi-finalsPlayer made it through to the 6th round (involving 4 players), but was eliminated there.	Quarter-finals GLOSSARY Quarter-finalsPlayer made it through to the 5th round (involving 8 players), but was eliminated there.	Round of 16 GLOSSARY Round of 16Player made it through to the 4th round (involving 16 players), but was eliminated there.	Round of 32	Round of 64	Round of 128
  Men’s Grand Slams	2000	1200	720	360	180	90	45	10
  Women’s Grand Slams	2000	1300	780	430	240	130	70	10
  Men’s ATP World Tour Masters 1000	1000	600	360	180	90	45	25	10
  Men’s ATP World Tour 500	500	300	180	90	45	20	-	-
  Men’s ATP World Tour 250	250	150	90	45	20	10	-	-
  Women’s Premier Mandatory	1000	650	390	215	120	65	35	10
  Women’s Premier 5	900	585	350	190	105	60	1	-
  Women’s Premier	470	305	185	100	55	30	1	-

The WTA currently awards players in a 2016 Grand Slam tournament 780 points for being eliminated in the semi-finals, 1,300 points for being eliminated in the final and 2,000 points for winning the tournament; the points almost double for every extra round that a player progresses. This is an example of exponential growth, a mathematical process that causes numbers to grow rapidly.

At the time of writing, Samantha Stosur is the highest-ranked Australian women’s tennis player. In 2015, Stosur was eliminated in the round of 64 in the Australian open (earning 70 points), the round of 32 in the French Open (earning 130 points) and Wimbledon (another 130 points), and the round of 16 in the US Open (earning 240 points). So, at the very start of 2016, the Grand Slam tournaments contributed 70 + 130 + 130 + 240 = 570 points towards Stosur’s combined ranking points (for singles tennis) for the previous 52 weeks.

Seeding a tournament

Once the players are ranked, seeding a tournament can just be a matter of listing the top 32 entrants in order of ATP or WTA rankings. This is how the Australian Open, French Open and US Open tournaments are seeded. Wimbledon, however, chooses to do things a little differently. Instead of using the ATP ranking points, they use their own modified points calculated using the formula:

$$\text{Ranking points} = \text{ATP} + G_{\text{all}} + \left(75 \% \times G_{\text{best}} \right)$$

where:

• ATP is the total ATP points accumulated by the player until the Monday before the tournament starts
• G_all is the total number of points earned for all grass court tournaments in the past 12 months
• G_best is the number of points awarded for the player’s best performance at a grass court tournament in the 12 months before that.

As Wimbledon is played on grass courts, the formula is designed to give more weight to ranking points that players earned on grass courts. Interestingly, Wimbledon bases their seeding for the women’s tournament on the unmodified WTA rankings, in line with the other Grand Slams.

Structuring a tournament

Once the top players have been seeded, there are two main considerations that determine how tennis tournaments are structured.

First, the number of matches needs to be kept to a manageable level. Grand Slam tournaments start with a field of 128 players. If we design a tournament in which every player plays a match against every other player, then every single player would have to play at least 127 matches throughout the tournament (exhausting!) and there would be at least 8,128 matches in total. The tournament would have to run over most of the year!

• Where did the number 8,128 come from?

  A branch of mathematicians called combinatorics is used by mathematicians to quickly count things without actually having to count them one by one. For instance, how many tennis matches would need to be played before every player in the field of 128 has played every other player? This is the same as asking how many possible pairs of players we can make by choosing 2 players out of the 128.

  Let’s imagine the two players standing next to each other… 

  $$\_\_\_ \; \_\_\_$$

  Now we have to select the players. We start by choosing the first player in the pair. How many choices do we have? There are 128 players in the tournament, so we have 128 options for the first player … 

  $$128 \; \_\_\_$$

  Next, we choose the second player in the pair. How many choices do we have now? Well, we’ve already picked out 1 player, so that leaves 127 players left to choose from … 

  $$128 \; 127$$

  Now for each of the 128 choices of the first player, we can make 127 selections of the second player. So the total number of possible pairs is

  $$128 \times 127$$

  But wait, we counted too many pairs! Here’s the problem: choosing Federer first and Djokovic second gives us the same pair of players as choosing Djokovic first and Federer second. So we’ve actually counted each pair twice. To reach the correct number of pairs, we have to halve our count …

  $$\frac{128 \times 127}{2}$$

  which is 8,128. With this method we can find the answer to our question without having to count each combination individually.

Can we do better? What is the fewest number of matches that we need in the tournament?

If we assume that a player has to lose at least one match in order to be knocked out of the tournament, then no matter how we structure the tournament we’re going to need at least 127 matches. That is because we’re starting with a field of 128 players, and 127 of them have to be knocked out before we can determine the winner.

Can we design a tournament that determines a winner after precisely 127 matches? Yes, we can, and it’s surprisingly straightforward. We use what is called a ‘single-elimination’ tournament structure (or what mathematicians who study graph theory might call a ‘binary tree’).

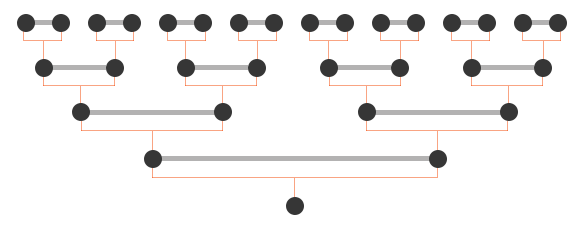
In a single-elimination (or knockout) tournament, the winners of each round progress to the next round while the runners-up are immediately eliminated. In this simplified diagram (showing only 16 players), each circle represents a player; the line between players represent a match; and only the winner will advance to the next match.

This tournament features the mathematical process of exponential decay—half the players that start any given round are knocked out by the end of that round, which causes the number of players left in the tournament to drop off rapidly as the tournament progresses. The winner and runner-up of the whole tournament only need to play 7 matches, and every other player in the tournament players fewer matches. With the minimum number of 127 matches played, the Grand Slam tournaments can be held in a very reasonable timeframe of 2-3 weeks.

• Why do Grand Slam tournaments have 128 entrants?

  If we use a single-elimination tournament structure and want to avoid byes (having some players sit out the first round), then the number of tournament entrants must be a power of 2 GLOSSARY power of 2The number 2, multiplied by itself several times. A power of 2 looks like 2^x, which means means ‘take x lots of 2 and multiply them all together’. So 2¹ is 2, 2² is 2×2, 2³ is 2×2×2, and so on. .

  To see this, note that we have exactly 1 winner, so the last round involves 1 final match involving 2 players—and those 2 players must have won their respective semi-finals. So there must have been 2 semi-final matches played in the previous round, involving 4 players in total—and those 4 players must have won their respective quarter-finals. So there must have been 4 quarter-final matches played in the previous round, with 8 players in total … and the pattern emerges! Since the number of players halves as we progress through the rounds (the winners keep playing, while the runners-up are eliminated), the number of players must double as we move backwards from the final to the first round.

  All that doubling means that our number of starting players must be 2, 4, 8, 16, 32, 64, 128, 256 or larger powers of 2. Grand Slams have 128 players because it’s the ‘Goldilocks’ option—not too few players (as 64 would be), not too many (as 256 would be), it’s ‘just right’.

The second thing to consider is that, ideally, the tournament should become more difficult for the players as the rounds progress—players should be more likely to encounter higher-ranking players later in the tournament. This will naturally happen as stronger players triumph in their rounds, but we need to be careful in our tournament design: we want to make sure that the top seeds don’t meet each other (and knock each other out) at the start of the tournament, so we place the seeded players carefully in tournament brackets. The first and second seeds are placed at the very ends of the first round, like so:

The first and second seeded players are placed far from each other in the first round of a tournament.

This ensures that, if the first and second seeds win all of their matches, they can’t face each other until the finals. A similar idea is used to make sure the top 4 seeds can’t meet each other until the semi-finals—seeds 3 and 4 are placed (randomly) in the following two positions.

The third and fourth seeded players are placed to avoid early matches with each other (or with the first and second seeded players).

Likewise, none of the top 8 seeds can meet until the quarter-finals, the top 16 won’t meet until the fourth round and the top 32 seeded players won’t meet until the third round. The remaining 96 unseeded players (8 of which are ‘wild card’ entries to the tournament, selected on other grounds than their world ranking) are then placed randomly in the remaining slots. This careful setup of the tournament draw is why you never see two big-names clashing until the later stages of the tournament. 

Scrutinising the scores

Moving from tournament organisation to analysis of the game itself, perhaps the most striking feature of tennis is its unique scoring system. It turns out that it’s not just a quirky flavour—the division of a match into points, games and sets actually impacts the final results in some unexpected ways.

• Terminology and the scoring system

  Match

  A tennis match is broken up into 3 sets (except for matches in the men’s Grand Slam tournaments, which are broken up into 5 sets). The first to win 2 of the 3 sets (or 3 of the 5 sets) wins the match.

  Sets and tie-breakers

  A set is broken up into games. A set is over once a player/team has won at least 6 games with a winning margin of at least 2 games. Usually, if both sides have won 6 games apiece in a set, the set is resolved by a tie-breaker (which is won by reaching at least 7 points with a winning margin of at least 2 points). Tie-breakers are not used in the fifth set of a match (except at the US Open, the only Grand Slam which uses a tiebreak in the final set).

  Games and serve

  A game is a collection of points in which one side serves throughout and the other side receives throughout. If the serving side wins the game, they are said to have held serve. If the receiving side wins the game (which is usually harder to do but necessary to win the set), they are said to have achieved a break of serve. The serving side and the receiving side switch at the end of every game.

  Points

  A point is the basic scoring unit in tennis, gained by the side that hits a successful shot that their opponent is unable to return successfully. The first side to win at least 4 points with a winning margin of at least 2 points wins the game. Points in tennis are read 0 (love), 15 (fifteen), 30 (thirty) and 40 (forty) to mean 0, 1, 2 and 3 points, respectively. Points are called out in order of the side currently serving first, followed by the side currently receiving. If the umpire calls forty-fifteen at the end of a point, it means that the serving side currently has 3 points and the receiving side currently has 1 point. 

  Deuce and advantage

  A score of forty-all (3 points for each side) is called deuce. The side to win the following point after deuce is said to have the advantage (needing to win only the next point to win the game). After a side has the advantage, they will either win the game (if they win the next point) or the score will return to deuce (if the team without the advantage wins the next point).

  Scores

  Tennis scores are reported in terms of the number of games won in each set (and the points in the current game, if the match is still in progress). A typical score might look like:
  $$\text{Alice v Bob: } \quad 6\text{-}4 \quad 6\text{-}7 \quad 6\text{-}1$$ This would mean that Alice won the first set (winning 6 games to Bob’s 4), then Bob won the second set (by winning the tie-breaker after the score reached 6-6 in the second set), and finally Alice won the third set with 6 games to Bob’s 1. Since Alice won 2 of the 3 sets, she won the match.

A surprising paradox

One of the key features of the tennis scoring system is that, unlike sports such as cricket or football, not every point ultimately affects the outcome of the match. To see how this works, consider a match between Alice and Bob in which Alice is serving the first game of the first set. Alice wins the first 3 points, so at that stage the score is 40-0. 

If Alice wins the next point, she wins the game, and the overall score for the match sits at 1-0.

But suppose Bob manages to score the next 2 points instead. The score sits at 40-30. Alice then wins the next point, she wins the game—and the overall score for the match again sits at 1-0. The same outcome occurs both times, regardless of whether or not Bob won his two points! Bob’s two points were effectively erased once Alice won the game, and have no influence whatsoever on the final outcome of the match.

This can lead to strange situations in which players can win more points than their opponents—or even more games—and yet still lose the match! This surprising result is closely related to a phenomenon in statistics called Simpson’s Paradox, where looking at data in greater detail can lead to different conclusions than looking at data on a broad scale. How often does this actually occur in professional tennis matches? A study in 2013 set out to answer this question by analysing 61,000 professional tennis matches over a 21 year timespan. It found that about 4.5 per cent of games were won by the players with fewer overall points (so roughly 1 game in 22).

One of the most famous examples of this phenomenon occurred in the first round of Wimbledon in 2010, when American player John Isner defeated French player Nicolas Mahut, despite Isner winning fewer points overall (Isner won 478 points and Mahut won 502). The final score for the match was 6-4, 3-6, 6-7, 7-6, 70-68 (remember: no tie-breakers in the fifth set at Wimbledon). This match also holds the record for the longest tennis match in history: 11 hours and 5 minutes spread across 3 days. A plaque commemorating this feat remains on Wimbledon Court 18.

Matches where the losing player wins more games (as opposed to points) are more rare, but still possible. In the final match of the 2009 Wimbledon Championship, Swiss player Roger Federer defeated American player Andy Roddick, despite Federer winning 38 games to Roddick’s 39 games. The final score was 5-7, 7-6, 7-6, 3-6, 16-14.

So why not switch to a simpler scoring system where only the total number of points matters? Tradition (and quirky flavour) aside, it turns out that the same mechanism that allows players to win with fewer points may also give consistently better players a better chance to win the match.

Winning probabilities

Mathematicians use Markov chains to analyse any system that moves from one state to another with certain probabilities. In his 1989 book Game, Set and Math, British mathematician Ian Stewart used the mathematics of Markov chains to analyse a model tennis match. He found that if one player has probability p of winning any given point (which means their opponent has probability 1−p of winning any given point), then the probability that that player would win any given game was not p. Instead, it was given by the formula:

$$p^4 + 4p^4(1-p) + \frac{10p^4(1-p)^2}{1-2p(1-p)}$$

What does this mean? If p=0.5, so both players are equally likely to win a point, then the probability that either player wins the game is also 0.5, as expected. However, the graph of this function has an interesting shape.

Winning probabilities

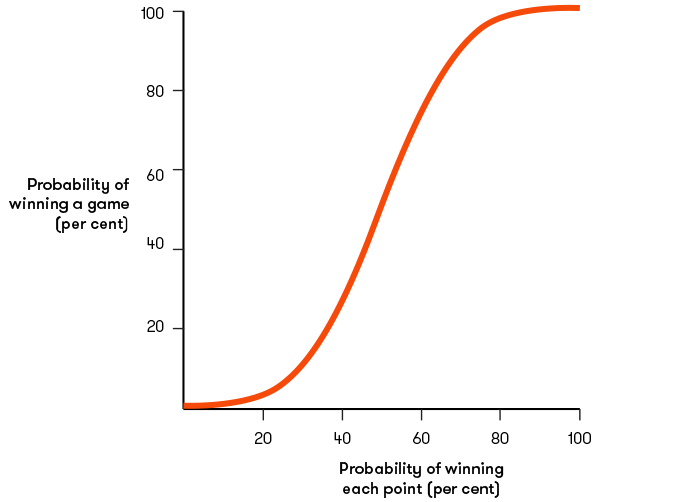
The graph shows that if the probability of winning a point differs from 0.5 (or 50 per cent) by just a little bit, the probability of winning a game changes by a lot. If the probability of a player winning each point moves up to 60 per cent, the probability of winning each game jumps up to over 73 per cent. A 70 per cent chance of winning each point translates into a 90 per cent chance of winning each game.

Stewart also found other formulas linking the probability of winning each individual point to the probabilities of winning sets and the match. The effect is magnified as we move from games to sets to matches.

Note that this model is only a simple model. In particular, analysis of professional tennis matches shows that the probabilities of each player winning a given point does not stay the same throughout the match, but changes based on the outcomes of previous points. Nonetheless, it is useful to note that the scoring system of tennis rewards players who can maintain a consistent edge over their opponents, even if the edge is only small.

Ongoing developments

Mathematicians have served up many papers concerning tennis, and it remains an active area of research to this day. We are continuing to learn more about the effects of the scoring system and how it might be made fairer, the best strategies for players to adopt, the impact of the home-court advantage and many other topics. The game is continually changing as new technologies—such as the Hawk-Eye system for tracking ball trajectories—are introduced. The aspects we’ve covered in this article are just the opening points in tennis maths.