To infinity
Expert reviewers
Essentials
- In its simplest sense, infinity refers to the concept of ‘forever’ or ‘without end’.
- Mathematicians treat infinity as a transfinite cardinal number, which is very different from a regular number. Cardinal numbers are used to describe the sizes of sets.
- Sets that have the same size as the set of natural numbers are called countably infinite. Examples include the set of even numbers, the set of square numbers and the set of all prime numbers.
‘To infinity … and beyond!’ It’s the iconic catchphrase of Buzz Lightyear, the heroic space ranger from Pixar’s Toy Story.
But from a mathematical standpoint, does travelling beyond infinity make sense? What does the concept of infinity actually mean? Questions surrounding infinity have occupied some of the world’s greatest thinkers for millennia, and the answers they’ve found may surprise you.

The idea of infinity
Our starting point is a branch of mathematics called set theory. A mathematical set GLOSSARY mathematical seta collection of objects (or elements). The order of these objects in the set does not matter, and each object is included only once. is like a box: it’s a container for a bunch of objects, called elements, which can be pretty much anything. Mathematicians use curly brackets to denote sets and place their elements inside the brackets in no particular order. Those sets are given a capital letter to represent them. For instance, the set P of rocky planets in our solar system could be written as:
$$\text{P = \{Mercury, Venus, Earth, Mars\}.}$$
The size of a set is given by the number of elements, in this case 4. The size is technically known as its cardinality, and is described using cardinal numbers GLOSSARY cardinal numbersnumbers used to denote the size of sets. . The cardinal numbers that define finite sets are familiar counting numbers like 0, 1, 2, 3 and so on.
Sets can be considered the most basic building blocks in mathematics. Numbers themselves are even constructed out of sets.
Mathematicians use the concept of infinity to describe a feature of certain sets, like the set containing all the natural numbers. But not all sets are infinite. The set of all single-digit natural numbers starts at 0 (or 1, depending which mathematician you ask) and stops at 9:
$$\text{\{0,1,2,3,4,5,6,7,8,9\}}$$
On the other hand, the set of all natural numbers is infinite. If you tried to write out a list of all the natural numbers, you’d have to write forever.
$$\text{\{0,1,2,3,4,5,6,7,8,9,10,11,12, … \}}$$
This is infinity in a nutshell. In its simplest sense, infinity is not anything like ‘an unimaginably huge number’ or ‘the largest possible number’. Infinity is not a number, it is an idea—the idea of ‘forever’ or ‘without end’; the idea that you can keep counting as long as you like without ever reaching a largest number and having to stop.
The story doesn’t stop here though—it’s only just getting started.
Infinity versus infinity
Mathematicians have grappled with the concept of infinity for millennia, since at least the time of the Greek philosopher Zeno of Elea and his famous paradoxes almost 2,500 years ago. The Italian scholar Galileo also confronted the weird and downright paradoxical nature of infinity in the 17th century. Galileo noted that, mathematically speaking, there seemed to be precisely the same amount of natural numbers as square numbers GLOSSARY square numbersnumbers that are formed by squaring the natural numbers (multiplying them by themselves). The first five square numbers are 1, 4, 9, 16 and 25. , even though it intuitively seemed like the natural numbers should vastly outnumber the square numbers. Comparing different infinite sets seemed fraught with mathematical peril.
Thanks to some groundbreaking work in the late 19th century—mostly due to German mathematician Georg Cantor—we now have a firm grasp on the nature of infinity. Not only that, but mathematicians routinely (and safely) use infinity in their calculations, and have rigorous ways of treating infinity as a type of mathematical object known as a ‘transfinite cardinal number’ (which behaves very differently to finite cardinal numbers like 0, 1, 2 and so on).
Transfinite cardinals allow us to accurately compare different infinite sets, leading to the stunning conclusion that some infinite sets are, in fact, bigger than others! (Though not Galileo’s set of natural numbers and set of square numbers, which really are the same size.)
To see how this is possible, let’s first think about how we compare the size of finite sets. We have two fundamentally different methods of doing this—evaluating their cardinalities by counting, or trying to pair off elements between the sets. It’s simpler than it sounds!
Comparing cardinalities
The first method, counting the elements in each set and then evaluating their cardinalities, is probably how you would instinctively compare the size of two different sets. Let’s break down the mathematical process that’s going on.
First, we have to enumerate the elements in each set—that is, we have to explicitly list each and every single element contained in a set, in some order. Then, we count along the list of elements and label them ‘first’, ‘second’, ‘third’ and so on (although we may just say ‘one’, ‘two’, ‘three’ instead of ‘first’, ‘second’, ‘third’), until we reach the end of our list. We then label the set with a natural number—its cardinality—according to how many elements we counted.
Once you’ve done this for each set, you can compare the cardinalities to determine which set is bigger or if they’re the same size.
Let’s look at an example of comparing cardinalities. Imagine you invite some friends over for dinner. Just before everyone arrives, you worry that you don’t have enough chairs to seat everyone. You want to compare the cardinality of the set of people with the cardinality of the set of chairs.
First you list the number of people coming for dinner, in any order—Adam, Bianca, Charlie and yourself. Then you count along that list: one, two, three … four people. The set of people has cardinality 4.
You then count the number of chairs. For no particular reason, you start at the head of your table and work clockwise: one, two, three … four chairs. The set of chairs has cardinality 4.
Comparing the cardinalities, you notice that there are the exactly the same number of people as chairs, and you breathe a sigh of relief.
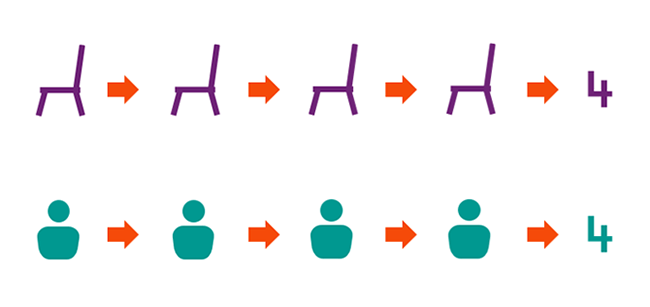
This process may seem obvious, but there’s a snag—this method relies on us being able to enumerate each set (to explicitly list every element). This is not always practical when the sets are large, and not possible when the sets are infinite! Fortunately, we have another method of comparing sets.
Pairing off elements
Let’s take another example. This time, imagine you’re walking onto the stage of a large theatre to thunderous applause. As you do so, you wonder if the theatre is packed out. You want to compare the cardinality of the set of people in the audience with the cardinality of the set of seats in the theatre.
You begin to enumerate the members of the audience … but no, there’s too many of them! It will take you far too long, and it might become awkward if you’re still working this out when the applause dies down.
Instead, you try a different approach—you look out into the crowd and begin to pair off people with seats. It quickly becomes apparent that every person in the audience can be matched with a seat (no-one has been left standing), and every seat in the theatre can be matched with a person (no seat has been left empty).
By linking the elements of each set with exactly one element from the other set, and having no elements left without a partner, you have just created a ‘bijection mapping’ between the set of people and the set of seats. As you may have guessed from the ‘bi’ in ‘bijection’, this mapping goes both ways—no matter whether you look at a person or a seat, there’s going to be a partner from the other set that uniquely matches.
With this mapping, you know that there are the same number of people as there are seats—even though you can’t say precisely how many people and seats there are.
If you hadn’t been able to match every element between the sets, you could still draw a conclusion. If there had been extra seats left over after every person had been matched with a seat, for instance, you would know that there were more seats than people. (The partially complete pairing would be called an ‘injection’.)
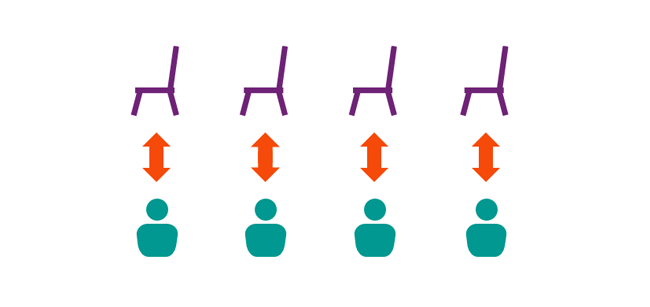
Crucially, setting up a bijection doesn’t require us to list out every single element in each set—we just have to pair up the elements in each set. So this approach can be applied to infinite sets as well.
Odds and evens
With our knowledge of bijections, let’s compare the size of some infinite sets to see which ‘infinity’ is bigger. First, consider the set containing all the odd numbers (let’s call it O):
$$\text{O = \{1,3,5,7,9,11, …\}}$$
and the set containing all the even numbers (let’s call it E):
$$\text{E = \{2,4,6,8,10,12, …\}}$$
Even though these sets are both infinite, we might intuitively expect them to be the same ‘size’—to have the same cardinality. To check that this is the case, we’ll build up a bijection between the sets.
We can pair off each odd number with the even number immediately after it, and therefore we also pair off each even number with the odd number immediately before it. To pick a few examples, 1 and 2 are paired up, 3 and 4 are paired up, 343 and 344 are paired up, and so on.
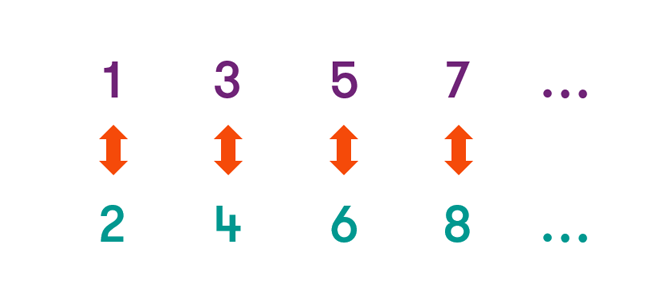
With this matchmaking system, every odd number has a unique even partner and every even number has a unique odd partner. Nothing has been left unpaired. If you pick any odd number in O you can easily determine its matching partner in E, and vice versa. Therefore, we can say that the two sets O and E have exactly the same cardinality, even though we can’t put a figure on how many elements are in the sets.
Even odder
It makes intuitive sense that the set of odd numbers and the set of even numbers should be the same cardinality. Yet, when it comes to infinity, things can become strange and our intuition can fail us.
For our next example, let’s think about comparing the set of natural numbers, called ℕ (let’s leave 0 out this time):
$$\mathbb{N}\text{ = \{1,2,3,4,5,6, … \}}$$
with the set of even numbers:
$$\text{E = \{2,4,6,8,10,12, … \}}$$
We might expect the set of natural numbers to have a larger cardinality than the set of even numbers—but this is not the case! We can build a bijection between ℕ and E if we pair off each natural number with the even number that’s twice as large, and therefore pair each even number off with the natural number that’s half as large. To pick a few examples, 1 and 2 are paired up, 2 and 4 are paired up, 3 and 6 are paired up, and so on.
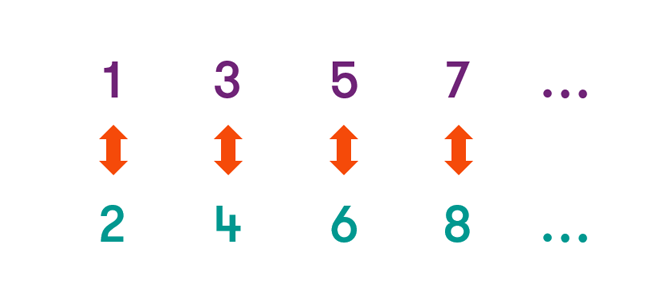
Under this system, every natural number has a unique even partner, and every even number has a unique natural-number partner. Nothing has been left unpaired—you can pick any element in ℕ and quickly determine its partner in E, and vice-versa. Therefore, we can say that the two sets ℕ and E have the same cardinality.
In fact, we can put a label on this cardinality. It’s not going to be a finite cardinal number, like 0, 1, 2, and so on, so it will have to be something completely different: a transfinite cardinal number.
The set of natural numbers (ℕ) and any set that can be matched perfectly with it (like O and E) have a cardinality we call ℵ0 (pronounced ‘aleph-null’). This is our first example of a transfinite cardinal number, and it’s the ‘infinity’ that most people know best.
Any set that has a cardinality of ℵ0, such as the set of counting numbers, is said to be ‘countable’ or ‘countably infinite’. That’s because a bijection between a countable set and the set of natural numbers lets you ‘count’ the elements in the set, labelling an element with 1, another element with 2, and so on.
This brings us to Galileo’s example: the set of square numbers also has cardinality ℵ0. Every natural number can be squared to match it with a square number, and taking the square root of a square number will take you to its natural-number-partner. There really are as many square numbers as natural numbers—or, more precisely, those two sets have the same cardinality, ℵ0.
Infinities of the same size
Many infinite sets actually have the same size (the same cardinality). Select two possible sets to see how we can match up their elements exactly (building a bijection between the sets). You can also enter a specific number from one set to see what it was paired up with.
Select two infinite sets
Here’s how the first few match up
| Odd | 1 | 3 | 5 | 7 | 9 |
|---|---|---|---|---|---|
| Even | 2 | 4 | 6 | 8 | 10 |
| Even | 2 | 4 | 6 | 8 | 10 |
|---|---|---|---|---|---|
| Natural | 1 | 2 | 3 | 4 | 5 |
| Natural | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Square | 1 | 4 | 9 | 16 | 25 |
Try it out
Insert a number then click ‘calculate’ to show what it can be uniquely mapped to.
Conclusion
To compare the size of infinite sets we try to build a bijection—we link every element of each set with exactly one element from the other set, with no elements left over. By pairing up elements we can discover surprising results, like that the set of all natural numbers is the same size as the set of all even numbers, and the set of all square numbers, and even the set of all prime numbers! They are all the same ‘countably infinite’ size, with cardinality ℵ0.
From the examples we’ve seen here, it seems like all the possible infinite sets might just share the same cardinality—our familiar infinity, ℵ0. For a long time, mathematicians thought this was the case—but, as it turns out, they were wrong! Read on to discover the different sizes of infinity.